There are lots of literature dealing with sampling methods (probabilistic as well as purposive sampling) and resampling techniques. Whereas the in the first ones the focus is posed in the representativity of the sample (i.e., how well the “miniature” of the population is reflected in those selected units), resampling methods mostly try to enhance the precision of the estimates, for instance mean, relative standard deviation, bias, etc.

The purposive selected samples (subjective) rely on non-randomized techniques, so they are prone to show considerable biases and are out of the scope of this article. On the contrary, probabilistic samples applies randomization in the selection of sample units, keeping bias under more control or else reducing it to negligible impact on the inferences performed.

This article intends to be a rehearsal on basic concepts regarding sampling and resampling methods, so as the reader can have a quick glance of the classic methods and more common resampling available techniques. It is focused to bring more intuitive concepts rather than mathematic developments, which are only applied in its minimal expression when necessary to gather the concepts.

• Classic Sampling Methods

The classic sampling methods belong to those called probabilistic, in which the elements are selected using a procedure that brings each one a positive (not zero) and known probability of being included in the final sample. Amongst the most known, there are: randomized single sampling, systematic sampling, stratified sampling, and conglomerate sampling, which are summarized below:

Randomized Single Sampling:

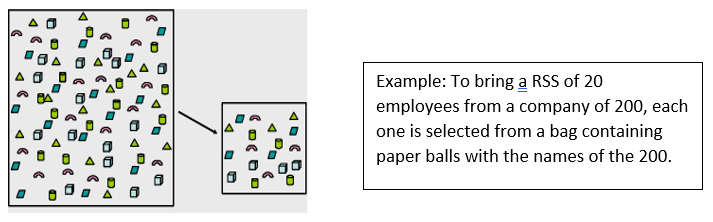
In this model, all elements have the same probability of resulting elected, and all subsets of n elements is a possible sample. It is not needed to know the size of the universe (N), but only respecting the condition that n < N.

Systematic Sampling:

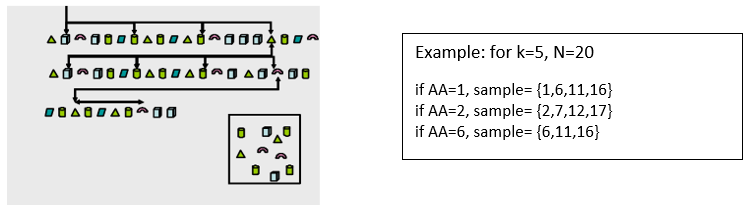
This sampling method takes one element each k units, where k is the selection interval and an integer. After selecting a randomized start (AA), sample elements are obtained this way: AA; AA+k; AA+2k…

It has the particularity that the different samples do not repeat their elements and may not have the same quantity of them.

Stratified Sampling:

This approach enables to enhance the precision of a randomized single sampling by using auxiliary information to build strata, in other words, to segregate the population according to some pattern (e.g.: patient gender and age ranges in a hospital ward). By applying RSS in each stratum, intuitively the sample will be “shared” along the universe of cases, by selecting it proportionally to each strata considered.

Conglomerate Sampling:

In many situations, the obtention of a randomized sample by direct application of any of the previous methods is not possible or would result in a very expensive sample. Some situations include the lack of a sampling framework or a very disperse sample.

This type of sampling relies upon selecting several groups (conglomerates) of similar characteristics and then include some of them -completely- in the sample.

• Capture- Recapture

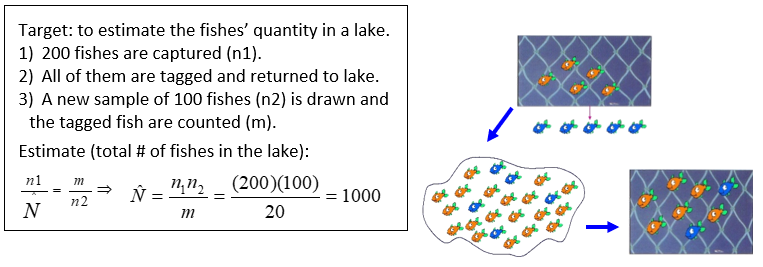
This method was originally developed to estimate the size of an animal population closed under a closed environment. The procedure can be resumed as follows: at a certain time as many animals as possible in an area are captured, tagged and then released (the ‘capture’ stage). At a later time this sample is repeated -the ‘recapture’ stage- counting both the tagged and not-tagged animals. The number of tagged animals in each sample, and the total number of animals of the second sample, are used to estimate the number in the total population assuming that capture and recapture are independent. Thus, the estimated probability of being captured on both occasions is equal to the product of the probabilities of being captured on each occasion.

An example:

• Jacknife

Developed by Quenouille in 1949, this approach is mainly used reduce/eliminate bias, to learn about the shape of the population distribution and/or when there is only one sample available (e.g.: lunar rocks). Assuming this unique sample is representative of the population, more samples are obtained by separating systematically one element from the original sample. Even that the main objective is to estimate variance and bias, this technique can also be used to get estimates of another measures like mean, confidence intervals, etc.

• Bootstrap

This technique was first introduced by Efron, 1979. The idea was as follows: when the distribution of the population is unknown, its best approach is the distribution of their samples’ values. It is applied for small samples and when asymptotic properties cannot be assumed.

Bootstrap is a technique that allows hypothesis testing and to generate confidence intervals, as well as to enhance sample reliability by reducing bias and the standard error. The technique can be resumed as follows: from the original sample, several random samples of size n are extracted with reposition (i.e., returning all elements of the previous sample to the original sample before taking next one), naming these new samples as bootstrap samples. For each of these “n” bootstrap samples (e.g.: 500 to 1500), the estimate of interest is calculated, obtaining B bootstrap estimate values. From them, the empirical frequency distribution of the estimate is obtained, which is a good approach of the original one.

There are several types of Bootstrap methods, depending on: a) the way to approach the population distribution, b) the way of taking samples of such population using this technique and c) the method to be used to calculate de confidence interval.

Schematically,

Conclusions

There is no golden standard to obtain a representative and reliable sample. Many times, it is not possible to use only one of the sampling techniques herein named and a mixture of them surely yields better results (in terms of bias and/or precision). However, the exposed methods are not limiting, as there are lots of derived work on each of them and several other sampling methods, some of them specifically developed for a particular situation.

The key is to select a suitable method that brings the more representative sample according to the scenario studied and the risk: benefit balance from the involved feasibilities (practical, economical, ethical, etc.).

Resampling methods are nowadays easy to apply with the help of informatics, and very useful to reduce bias and to obtain more precise inferences from a sample.